thztools.wave#

thztools.wave(n, *, dt=None, t0=None, a=1.0, taur=None, tauc=None, fwhm=None)[source]#

Simulate a terahertz waveform.

Parameters:

nint: Number of samples.
dtfloat or None, optional: Sampling time, normally in picoseconds. Default is None, which sets the sampling time to thztools.options.sampling_time. If both dt and thztools.options.sampling_time are None, the sampling time is set to 1.0.
t0float or None, optional: Pulse location, normally in picoseconds. Default is 0.3 * n * dt.
afloat, optional: Peak amplitude. The default is one.
taur, tauc, fwhmfloat or None, optional: Current pulse rise time, current pulse decay time, and laser pulse FWHM, respectively. The defaults are 6.0 * dt, 2.0 * dt, and 1.0 * dt, respectively.

Returns:

xndarray: Signal array.

Warns:

UserWarning: If thztools.options.sampling_time and the dt parameter are both not None and are set to different float values, the function will set the sampling time to dt and raise a UserWarning.

Notes

This function uses a simplified model for terahertz generation from a photoconducting switch [1]. The impulse response of the switch is a current pulse with an exponential rise time \(\tau_r\) and an exponential decay (capture) time, \(\tau_c\),

\[I(t) \propto (1 - e^{-t/\tau_r})e^{-t/\tau_c},\]

which is convolved with a Gaussian laser pulse with a full-width, half-maximum pulsewidth of fwhm.

References

[1]

D. Grischkowsky and N. Katzenellenbogen, “Femtosecond Pulses of THz Radiation: Physics and Applications,” in Picosecond Electronics and Optoelectronics, Technical Digest Series (Optica Publishing Group, 1991), paper WA2, https://doi.org/10.1364/PEO.1991.WA2.

Examples

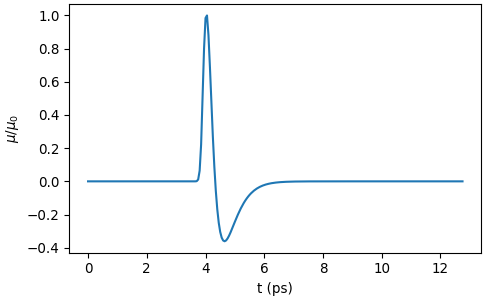
The following example shows the simulated signal \(\mu(t)\) normalized to its peak magnitude, \(\mu_0\).

>>> import thztools as thz
>>> from matplotlib import pyplot as plt
>>> n, dt = 256, 0.05
>>> t = thz.timebase(n, dt=dt)
>>> mu = thz.wave(n, dt=dt)

>>> _, ax = plt.subplots(layout="constrained")
>>> ax.plot(t, mu)
>>> ax.set_xlabel("t (ps)")
>>> ax.set_ylabel(r"$\mu/\mu_0$")
>>> plt.show()