thztools.NoiseModel.noise_var

method

NoiseModel.noise_var(x, *, axis=-1)

Compute the time-domain noise variance.

Parameters:

xarray_like

Time-domain signal array.

axisint, optional

Signal axis. Default is the last axis in x.

Returns:

noise_variancendarray

Time-domain noise variance, in signal units (squared).

Notes

For noise parameters \(\sigma_\alpha\), \(\sigma_\beta\), \(\sigma_\tau\) and signal vector \(\boldsymbol{\mu}\), the \(k\)-th element of the time-domain noise variance \(\boldsymbol{\sigma}^2\) is given by [1]

\[\sigma_k^2 = \sigma_\alpha^2 + \sigma_\beta^2\mu_k^2 \ + \sigma_\tau^2(\mathbf{D}\boldsymbol{\mu})_k^2,\]

where \(\mathbf{D}\) is the time-domain derivative operator.

References

[1]

Laleh Mohtashemi, Paul Westlund, Derek G. Sahota, Graham B. Lea, Ian Bushfield, Payam Mousavi, and J. Steven Dodge, “Maximum- likelihood parameter estimation in terahertz time-domain spectroscopy,” Opt. Express 29, 4912-4926 (2021), https://doi.org/10.1364/OE.417724.

Examples

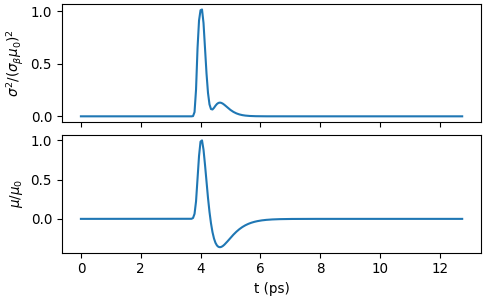
The following example shows the noise variance \(\sigma^2(t)\) for noise parameters \(\sigma_\alpha = 10^{-4}\), \(\sigma_\beta = 10^{-2}\), \(\sigma_\tau = 10^{-3}\) and the simulated signal \(\mu(t)\). The signal amplitude is normalized to its peak magnitude, \(\mu_0\). The noise variance is normalized to \((\sigma_\beta\mu_0)^2\).

>>> import thztools as thz
>>> from matplotlib import pyplot as plt
>>> n, dt = 256, 0.05
>>> t = thz.timebase(n, dt=dt)
>>> mu = thz.wave(n, dt=dt)
>>> alpha, beta, tau = 1e-4, 1e-2, 1e-3
>>> noise_model = thz.NoiseModel(sigma_alpha=alpha, sigma_beta=beta,
... sigma_tau=tau, dt=dt)
>>> noise_variance = noise_model.noise_var(mu)

>>> _, axs = plt.subplots(2, 1, sharex=True, layout="constrained")
>>> axs[0].plot(t, noise_variance / beta**2)
>>> axs[0].set_ylabel(r"$\sigma^2/(\sigma_\beta\mu_0)^2$")
>>> axs[1].plot(t, mu)
>>> axs[1].set_ylabel(r"$\mu/\mu_0$")
>>> axs[1].set_xlabel("t (ps)")
>>> plt.show()