Fit data with a frequency response function

Objects from thztools: apply_frf, fit, NoiseModel, timebase, wave.

import matplotlib.pyplot as plt
import numpy as np

import thztools as thz

from matplotlib.figure import figaspect
from scipy import stats

Set the simulation parameters

n = 256  # Number of samples
dt = 0.05  # Sampling time [ps]

sigma_alpha = 1e-4  # Additive noise amplitude [signal units]
sigma_beta = 1e-2  # Multiplicative noise amplitude [dimensionless]
sigma_tau = 1e-3  # Time base noise amplitude [ps]

p0 = (0.5, 1.0)  # Frequency response function parameters (amplitude, delay)

Simulate an input waveform

t = thz.timebase(n, dt=dt)
mu = thz.wave(n, dt=dt)

Define the frequency response function

The frequency response function frfun rescales the input waveform by a and delays it by eta.

def frfun(omega, a, eta):
    return a * np.exp(1j * omega * eta)

Apply the frequency response function

Generate the time-domain output waveform psi by applying frfun to mu with the apply_frf function.

psi = thz.apply_frf(frfun, mu, dt=dt, args=p0)

Add noise

Create an instance noise_model of the NoiseModel class and use the noise_sim method to add simulated noise to each waveform.

noise_model = thz.NoiseModel(
    sigma_alpha=sigma_alpha,
    sigma_beta=sigma_beta,
    sigma_tau=sigma_tau,
    dt=dt
)

x = mu + noise_model.noise_sim(mu, seed=0)
y = psi + noise_model.noise_sim(psi)

Fit the frequency response function to the noisy input and output waveforms

Fit the parameters of the frequency response function to the noisy input and output waveforms. The fitted parameters are consistent with the true parameters, and the goodness of fit statistic result.resnorm is consistent with a \(\chi^2\)-distribution with \(\nu = n_\mu - n_p - n_a - n_b = 253\) statistical degrees of freedom, where \(n_a = 1\) and \(n_b = 0\) because we exclude zero frequency.

result = thz.fit(frfun, x, y, p0, noise_parms=(sigma_alpha, sigma_beta, sigma_tau), dt=dt)
print(f"Amplitude parameter: {result.p_opt[0]:.4f} ± {np.sqrt(result.p_cov[0, 0]):.4f}")
print(f"Delay parameter: {result.p_opt[1]:.4f} ± {np.sqrt(result.p_cov[1, 1]):.4f}")
print(f"Goodness of fit: {result.resnorm:.1f}")
print(f"Degrees of freedom: {result.dof:d}")

Amplitude parameter: 0.4998 ± 0.0012
Delay parameter: 1.0002 ± 0.0005
Goodness of fit: 281.5
Degrees of freedom: 253

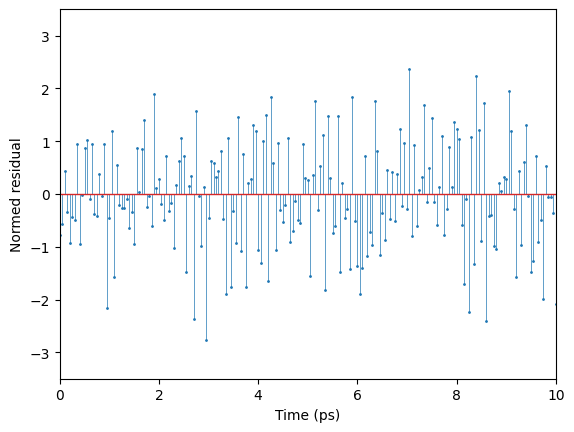
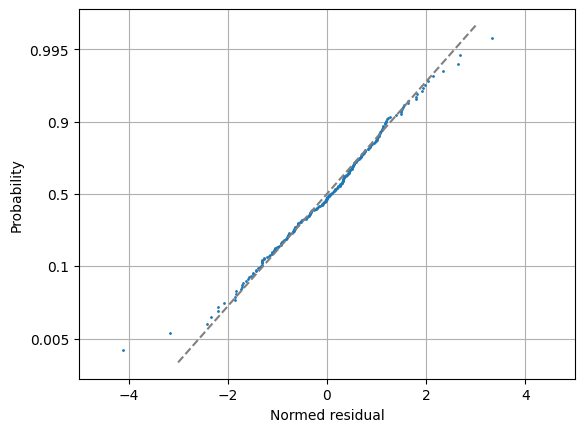
Show the fit residuals

As expected, the total-least-squares (TLS) residuals, result.r_tls, are Gaussian-distributed, and show no evidence of correlation in the time domain.

norm_res = result.r_tls
osm, osr = stats.probplot(
    norm_res, fit=False
)

_, ax = plt.subplots()

ax.plot(osr, osm, '.', ms=2)
ax.plot([-3, 3], [-3, 3], '--', c='gray')
ax.grid()

ax.set_xlim(-5, 5)
ax.set_ylim(stats.norm.ppf([0.0005, 0.9995]))

ax.set_xticks(np.arange(-4, 4.5, 2))
ax.set_yticks(stats.norm.ppf([0.005, 0.1, 0.5, 0.9, 0.995]))

ax.set_yticklabels(['0.005', '0.1', '0.5', '0.9', '0.995'])

ax.set_xlabel('Normed residual')
ax.set_ylabel('Probability')
plt.show()

_, ax = plt.subplots()

markerline, stemlines, baseline = ax.stem(
    t, norm_res, linefmt='-', markerfmt='.'
)
markerline.set_markersize(2)
stemlines.set_linewidth(0.5)
baseline.set_linewidth(1)

ax.set_xlim(0, 10)
ax.set_ylim(-3.5, 3.5)

ax.set_xlabel('Time (ps)')
ax.set_ylabel('Normed residual')

plt.show()